前回
kujira16.hateblo.jp
問題設定
行ったのはHondaらのAISTATS 2014の論文 [1] の中の実験の追試で，報酬が 
, 
の正規分布に従うアームと 
, 
の正規分布に従うアームがそれぞれ1本ずつあるという設定の多腕バンディット問題です。
原理
最初にパラメータ 
を -1/2, 0, 1/2 あたりの値に設定します。 については後述します。
Thompson Samplingを始める前に，まずそれぞれのアームを 
回引いておきます。このとき得られた報酬も個々のアームについて記録しておきます。
この後からは，個々のアーム 
についてStudentの 
分布 
から乱数を発生させ，最も大きい乱数が得られたアームを選択します。ここで 
はアーム を引いた回数，
はアーム から得られた報酬の標本平均，
はアーム から得られた報酬の標本標準偏差（Nで割るほう）です。
Studentの 分布はどこから出てくるのかというと，データ 
が得られたもとで平均 
と標準偏差 
が未知の正規分布のパラメータの分布 
をベイズの定理から計算し，これを について周辺化すると出てくるようです [2]。このとき，事前分布 
の設定方法には諸説あるらしく，一様分布を設定したものが 
に，reference priorを設定したものが 
に，Jeffreys priorを設定したものが 
にそれぞれ対応するようです。
前回の実験では事前分布は結果にほとんど影響を及ぼさなかったのですが，今回の実験では違っていて，設定した事前分布によって結果が大きく異なっています。このあたりの難しい話については追えていないので [1] を参照してください。
以下のプログラムはコマンドラインでシード値と事前分布を与えるとThompson Samplingに従ってアームを10^4回引くシミュレーションを行うものです。報酬の標準偏差を計算するときには，得られた報酬の2乗の和を持っておけば ![\mathbf{Var}[X]=\mathbf{E}[X^2]-\mathbf{E}[X]^2](http://chart.apis.google.com/chart?cht=tx&chl=%5Cmathbf%7BVar%7D%5BX%5D%3D%5Cmathbf%7BE%7D%5BX%5E2%5D-%5Cmathbf%7BE%7D%5BX%5D%5E2)
を使って O(1) で計算できます。
package main
import (
"bufio"
"flag"
"fmt"
"math"
"os"
"github.com/leesper/go_rng"
"gopkg.in/cheggaaa/pb.v1"
)
var (
progress bool
prior string
seed int64
)
func init() {
flag.BoolVar(&progress, "progress", false, "")
flag.StringVar(&prior, "prior", "uniform", "")
flag.Int64Var(&seed, "seed", 0, "seed value for random generater")
}
type Rng struct {
gaussian *rng.GaussianGenerator
studentT *rng.StudentTGenerator
}
func NewRng(seed int64) *Rng {
return &Rng{
gaussian: rng.NewGaussianGenerator(seed),
studentT: rng.NewStudentTGenerator(seed),
}
}
func (rng *Rng) Gaussian(mu, sigma float64) float64 {
return rng.gaussian.Gaussian(mu, sigma)
}
func (rng *Rng) StudentT(nu int64, mu, sigma float64) float64 {
return sigma*rng.studentT.Student(nu) + mu
}
func IntMax(a, b int) int {
if a < b {
return b
}
return a
}
func ArgMax(xs []float64) int {
argmax := 0
for i := 1; i < len(xs); i++ {
if xs[argmax] < xs[i] {
argmax = i
}
}
return argmax
}
func gaussianBandit(rng *Rng, prior string) ([]float64, error) {
K := 2
mu := []float64{1, 0}
sigma := []float64{3, 0.3}
T := 10000
var alpha float64
switch prior {
case "uniform":
alpha = -0.5
case "reference":
alpha = 0
case "jeffreys":
alpha = 0.5
default:
return nil, fmt.Errorf("Unknown prior: %s", prior)
}
var bar *pb.ProgressBar
if progress {
bar = pb.New(T)
bar.Output = os.Stderr
bar.Start()
}
regret := make([]float64, T+1)
regret[0] = 0
N := make([]float64, K)
sum := make([]float64, K)
sum2 := make([]float64, K)
C := IntMax(2, 3-int(math.Floor(2*alpha)))
for k := 0; k < K; k++ {
for j := 0; j < C; j++ {
r := rng.Gaussian(mu[k], sigma[k])
N[k]++
sum[k] += r
sum2[k] += r * r
t := k*C + j
regret[t+1] = regret[t] + mu[0] - mu[k]
if progress {
bar.Increment()
}
}
}
for t := K * C; t < T; t++ {
muEstm := make([]float64, K)
for i := 0; i < K; i++ {
nu := int64(N[i] + 2*alpha - 1)
mu := sum[i] / N[i]
sigma := math.Sqrt((sum2[i]/N[i] - math.Pow(sum[i]/N[i], 2)) / float64(N[i]+2*alpha-1))
muEstm[i] = rng.StudentT(nu, mu, sigma)
}
k := ArgMax(muEstm)
r := rng.Gaussian(mu[k], sigma[k])
N[k]++
sum[k] += r
sum2[k] += r * r
regret[t+1] = regret[t] + mu[0] - mu[k]
if progress {
bar.Increment()
}
}
return regret, nil
}
func main() {
flag.Parse()
filename := fmt.Sprintf("%s/%s-seed%03d.txt", prior, prior, seed)
w, err := os.Create(filename)
if err != nil {
panic(err)
}
defer w.Close()
rng := NewRng(seed)
regret, err := gaussianBandit(rng, prior)
if err != nil {
panic(err)
}
bw := bufio.NewWriter(w)
defer bw.Flush()
for i, x := range regret[1:] {
fmt.Fprintln(bw, i+1, x)
}
}
シミュレーションは論文 [1] と同じようにシード値を変えて20000回行いました。事前分布とシード値の組合せを変更して実験を行う必要があるので，GNU Parallelがたいへん便利でした。
#!/bin/bash
set -ue
seq 1 20000 > seed.txt
printf "uniform\nreference\njeffreys" > prior.txt
cat prior.txt | xargs mkdir
parallel --bar "go run honda2014.go --seed {1} --prior {2}" :::: seed.txt :::: prior.txt
リグレットの変化のグラフを描画するためのPythonコードは以下のとおりです。シミュレーション結果のファイルサイズが大きいので，一度Pickleに書き出しました。
import seaborn
import scipy
import matplotlib.pyplot as plt
from tqdm import tqdm
from sklearn.externals import joblib
seaborn.reset_orig()
seaborn.set_context('talk')
seaborn.set_color_codes()
def load_grid(prefix, st, en, size=10000):
A = scipy.empty((size, en - st + 1))
for i in tqdm(range(st, en + 1)):
filename = f'{prefix}{i:0>3}.txt'
A[:, i - st] = scipy.loadtxt(filename)[:, 1]
return A
prefixes = ['uniform', 'reference', 'jeffreys']
for prefix in prefixes:
A = load_grid(f'{prefix}/{prefix}-seed', 1, 20000)
joblib.dump(A, f'{prefix}.pkl')
del A
plt.ylim(ymax=40)
plt.xscale('log')
plt.xlim(1, 10000)
fnames = ['uniform.pkl', 'reference.pkl', 'jeffreys.pkl']
labels = [r'$\alpha=-1/2$ (uniform)', r'$\alpha=0$ (reference)', r'$\alpha=1/2$ (Jeffreys)']
for fname, label in zip(fnames, labels):
A = joblib.load(fname)
ys = scipy.mean(A, axis=1)
del A
xs = scipy.arange(1, ys.shape[0] + 1)
plt.plot(xs, ys, label=label)
ys = scipy.log(xs)
coef = 1/(1/2*scipy.log(1+1/(0.3**2)))
plt.plot(xs, coef*ys, color='k', label='asymptotic bound')
plt.xlabel('plays')
plt.ylabel('regret')
plt.legend(loc='upper left')
plt.savefig('honda2014.png', dpi=100)
結果
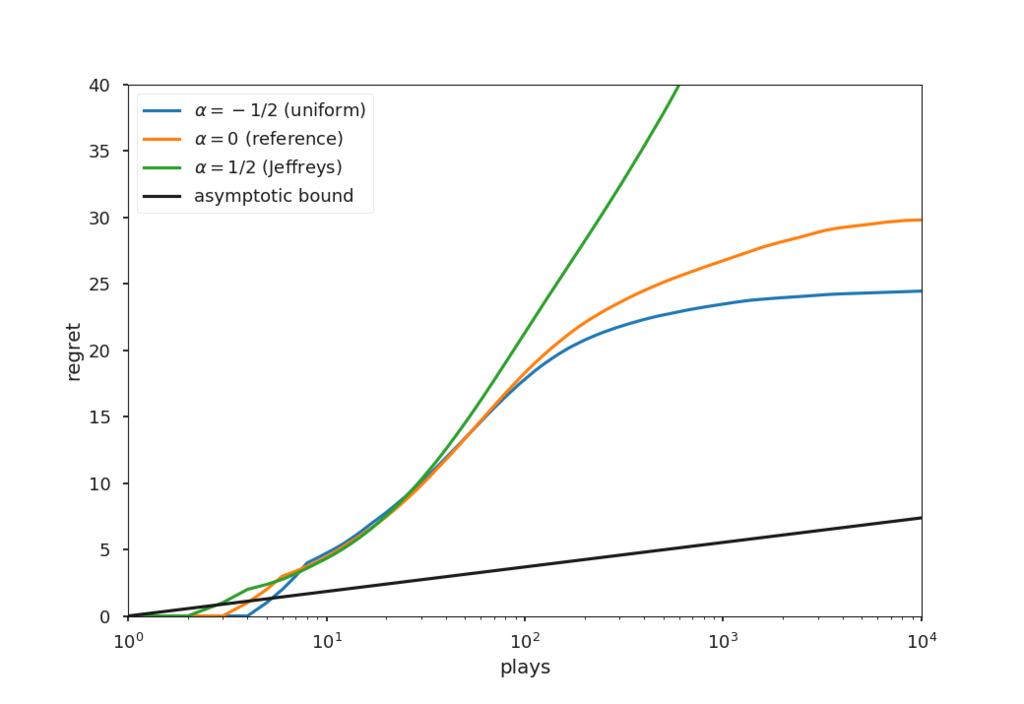
追試で欲しかった図は [1] p.4のFigure 1です。 によって性能が違っていますが，あくまでこれは期待値です。
参考文献
- [1] Honda, J. and Takemura, A.: Optimality of Thompson Sampling for Gaussian Bandits Depends on Priors, PMLR Vol.33 (2014) [PMLR] [arXiv].
- [2] Yang, R. and Berger, J. O.: A Catalog of Noninformative Priors (1998).
- [3] 本多淳也，中村篤祥：バンディット問題の理論とアルゴリズム，講談社（2016）．
575
