kd木のライブラリjtsiomb/kdtreeで最近傍探索を高速化してみた

次のような問題を解く必要がありました

3次元空間中に点群 $p_1, p_2, \dots, p_n$ と $q_1, q_2, \dots, q_m$ がある。ユークリッド距離が最小となるペア $(p_i, q_j)$ を報告せよ（決定的に振る舞うなら近似でもOK）

もっと良い方法もあるのかもしれませんが，今回はKD木を使って $O( (n+m) \log \min(n,m) )$ くらいの計算量で解くことにします。調べてみたところ，最近傍探索のライブラリとしては FLANN や nanoflann が有名なようです。

github.com

FLANNのドキュメントを流し読みしてみると，設定項目が禍々しく感じられたので，今回はこちらのライブラリを使ってみました。

github.com

このライブラリはとてもシンプルなので，今回の用途だと以下のAPIさえ使えればよいです。

kd_create で kdtree オブジェクトを作る
kd_insert で点群データを挿入する
kd_nearest で最も近い点を探す。戻り値の kdres * の内容は kd_res_item_data で読み取る。kdres * は kd_res_free で解放が必要。
kd_free で kdtree オブジェクトを解放する

このライブラリは内部で頻繁に malloc や free を呼び出しているので，今回解きたい問題では $n$ や $m$ が小さい場合にはオーバーヘッドが大きく， $O(nm)$ の総当りで解いたほうが高速な場合もありました。 $n=m$ の場合にサイズを変えながらナイーブな方法で解いた場合と比較した結果が以下の図です。

f:id:kujira16:20160303214425p:plain

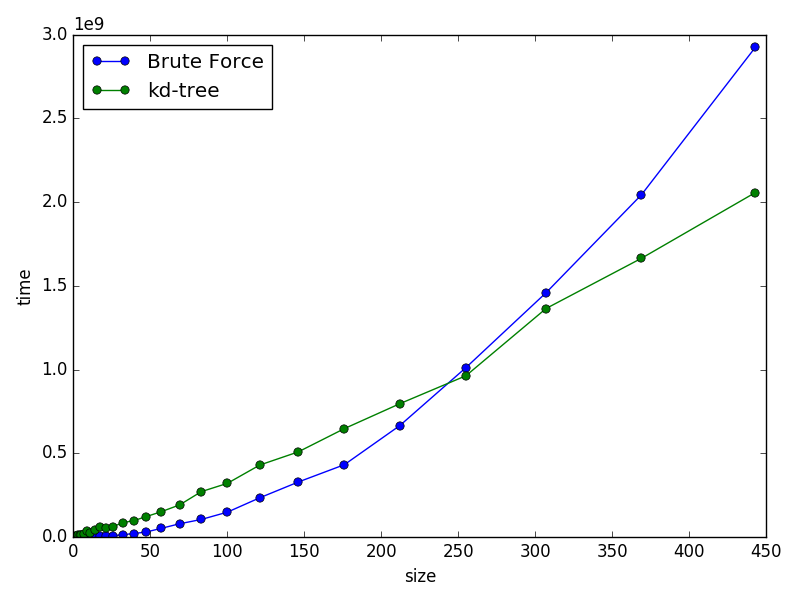
200〜300の間くらいで処理時間が逆転するようでした。適当にしきい値を決めて，データサイズによって処理を切り替えるような実装にするほうが良いと思います。

測定に使ったコードを以下に示します。std::vector や std::unique_ptr ではなく boost::scoped_array を使っているのは，いろいろと事情があるのです…

#include <cmath>
#include <cstdint>
#include <iostream>
#include <algorithm>
#include <vector>
#include <random>
#include <limits>
#include <boost/scoped_array.hpp>
#include "kdtree/kdtree.h"

uint64_t getCycle()
{
  uint32_t low, high;
  __asm__ volatile ("rdtsc" : "=a" (low), "=d" (high));
  return ((uint64_t)low) | ((uint64_t)high << 32);
}

struct Point {
  double x, y, z;
  Point(double x_, double y_, double z_) : x(x_), y(y_), z(z_) {}
};

double norm2(const Point &l, const Point &r) {
  const double dx = l.x - r.x;
  const double dy = l.y - r.y;
  const double dz = l.z - r.z;
  return std::sqrt(dx * dx + dy * dy + dz * dz);
}

static double useKDTree(const std::vector<Point> &left, const std::vector<Point> &right) {
  kdtree *tree = kd_create(3);

  boost::scoped_array<int> indexes(new int[left.size()]);
  for (int i = 0; i < (int)left.size(); ++i) {
    indexes[i] = i;
    kd_insert3(tree, left[i].x, left[i].y, left[i].z, &indexes[i]);
  }

  int l, r;
  double minimum = std::numeric_limits<double>::max();
  for (int j = 0; j < (int)right.size(); ++j) {
    kdres *set = kd_nearest3(tree, right[j].x, right[j].y, right[j].z);
    int i = *(int *)kd_res_item_data(set);
    kd_res_free(set);
    double d = norm2(left[i], right[j]);
    if (minimum > d) {
      minimum = d;
      l = i;
      r = j;
    }
  }

  kd_free(tree);
  return minimum;
}

static double bruteForce(const std::vector<Point> &left, const std::vector<Point> &right) {
  int l, r;
  double minimum = std::numeric_limits<double>::max();
  for (int i = 0; i < (int)left.size(); ++i) {
    for (int j = 0; j < (int)right.size(); ++j) {
      double d = norm2(left[i], right[j]);
      if (minimum > d) {
        minimum = d;
        l = i;
        r = j;
      }
    }
  }
  return minimum;
}

std::vector<Point> createRandom(const int num, const unsigned seed) {
  std::mt19937 eng(seed);
  std::uniform_real_distribution<double> distrib(-1000.0, 1000.0);
  std::vector<Point> v;
  v.reserve(num);
  for (int i = 0; i < num; ++i) {
    double x = distrib(eng);
    double y = distrib(eng);
    double z = distrib(eng);
    v.emplace_back(x, y, z);
  }
  return v;
}

int main() {
  const int n_iter = 1000;
  for (int num = 1; num <= 500; num = num * 1.2 + 1) {
    std::vector<Point> left = createRandom(num, 0);
    std::vector<Point> right = createRandom(num, 1);
    uint64_t clock_start, clock_elapsed1, clock_elapsed2;
    double sum = 0.0; // 最適化で処理が消えるかもしれないので，とりあえず和でも計算しておこうという考え

    clock_start = getCycle();
    for(int i = 0; i < n_iter; ++i) {
      sum += useKDTree(left, right);
    }
    clock_elapsed1 = getCycle() - clock_start;

    clock_start = getCycle();
    for(int i = 0; i < n_iter; ++i) {
      sum += bruteForce(left, right);
    }
    clock_elapsed2 = getCycle() - clock_start;

    std::cout << num << '\t' << clock_elapsed1 << '\t' << clock_elapsed2 << '\t' << sum << std::endl;
  }
}

くじらにっき++

kd木のライブラリjtsiomb/kdtreeで最近傍探索を高速化してみた

関連書籍